Discrete Conformal Maps as discrete integrable systems.
A discrete conformal map is a map ![]() with the property that
the cross-ratio of four adjacent points is constant. Specifically, for four points a,b,c,d on
with the property that
the cross-ratio of four adjacent points is constant. Specifically, for four points a,b,c,d on ![]() define their cross-ratio to be
define their cross-ratio to be
![]()
then the map is discrete conformal when
for some constant ![]() for all k,m.
More rigid definitions take q=-1. The motivation for this definition is
that if
for all k,m.
More rigid definitions take q=-1. The motivation for this definition is
that if ![]() is smooth then it is (weakly) conformal precisely when
is smooth then it is (weakly) conformal precisely when
![]()
i.e. when ![]() .
.
It is a remarkable fact that when the discrete map z has one period (i.e. ![]() for all k,m and some fixed period n) then it can be treated as an algebraically integrable dynamical system and may be written down in terms of the Riemann theta functions of an associated Riemann surface, called its spectral curve.
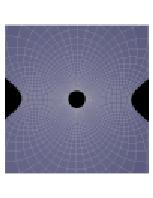
The pictures below are parts of discrete conformal maps with cross-ratio -1.
For these pictures the spectral curve is a rational curve with two nodes. These are
easy to compute with since the
for all k,m and some fixed period n) then it can be treated as an algebraically integrable dynamical system and may be written down in terms of the Riemann theta functions of an associated Riemann surface, called its spectral curve.
The pictures below are parts of discrete conformal maps with cross-ratio -1.
For these pictures the spectral curve is a rational curve with two nodes. These are
easy to compute with since the ![]() -function is a quadratic function of two exponentials.
-function is a quadratic function of two exponentials.
To see how this Riemann surface arises we consider the map as a discrete conformal flow of a discrete curve as follows.
 |
 |
 |
 |
 |