
The input file is a list of vertices:
# a triangular bi-pyramid 5 3 0 0 1 0 0 -1 1 0 0 -0.5 0.8660254 0 -0.5 -0.8660254 0The "5 3" at the beginning denontes 5 vertices and 3 dimensions. Following these two integers is the list of vertices. Pound-sign comments are accepted and whitespace is ignored.
Here is a sample output. The group order is 12.
The program uses some peculiar data structures and algorithms to find the group in screaming-fast time, no matter how many vertices are there are. Running time depends primarily on the group order, not the number of vertices.
Here is the man page.
If it hasn't crossed your mind yet, there is straightforward way to compute the symmetry group by choosing n independant vectors (n is the dimension) and running through all transformations defined by taking those n vectors to n other vectors, then checking if this transformation is orthogonal and fixes the set of points. If you have, say, 100 points in 4 dimensions, the algorithm would need to compute, among other things, 100 million matrix inversions. You don't want to do this.
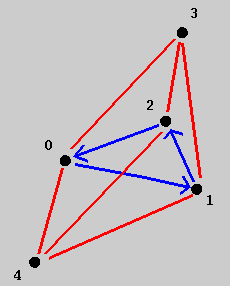
A graph is completely determined by its adjacency matrix. The input file for the graph above looks like this:
# adjacency matrix for a handed triangular bi-pyramid 5 0 b X r r X 0 b r r b X 0 r r r r r 0 X r r r X 0There is a blue arc from vertex 0 to vertex 1, so entry (0,1) has a "b". There is no arc the other way, from 1 to 0, so entry (1,0) contains an "X". The red arc from 2 to 3 goes both ways, so entries (2,3) and (3,2) both have an "r". The "5" at the beginning signals 5 vertices. Pound-sign comments are accepted. Whitespace is ignored. Here, all vertices have the same "color", meaning there is no distinction between vertices. If I wanted to denote vertex 2 as distinct from the others, entry (2,2) would contain a different string other than "0". The entries of the matrix are just strings; "X" is chosen arbitrarily in this example to denote no connection. The choice of "0" in the diagonal entries instead of "zero" or "jahosaphat" is also arbitrary.
Here is a sample output for the above graph. The group is the dihedral group of order 6. Notice the presence of directed edges has made the order half that of the space-group example above.
Here is the man page.
The source code will be out soon. I'm cleaning it up a little :-)
SGI binary for points in space (143K) (shift-click):
[spacegrp.gz]
SGI binary for graphs (47K) (shift-click):
[graphgrp.gz]
a perl script to convert a Geomview OFF file to a vfile: [off2v]
a perl script to convert an Evolver file to a vfile: [evol2v]
Back to my homepage.