New constant mean curvature cylindersAugust 16, 1999
IntroductionIn the article [5] Dorfmeister, Pedit and Wu presented a method by which all immersed CMC surfaces can, in principle, be constructed. Their construction is based on the observation that the Gauss map of every CMC surface is harmonic and every harmonic map from a surface D to S2 is the projection of a horizontal holomorphic map from its universal coverThe simplest known examples of CMC cylinders are the Delaunay surfaces, which are characterized by being cylinders of revolution (this includes the standard cylinder). From [7] one knows that if a CMC cylinder is complete and properly embedded then it must be a Delaunay surface. Also, every properly embedded annular end must be a Delaunay end (i.e. asymptotic to a Delaunay surface) even if the surface is not embedded. For example, the `bubbletons' studied by Sterling and Wente in [11] are immersed cylinders with no umbilics and both ends asymptotic to the standard cylinder. Their results lead them to pose the question: are there any CMC cylinders with umbilics? The examples we will present include cylinders which have one Delaunay end and any number of umbilics. In fact we present three new classes of CMC cylinders. The first class includes surfaces which are best thought of as a Smyth surface [10,5] with the head replaced by a Delaunay end. Given the results of [12] on Smyth surfaces we conjecture that these new examples are complete and proper immersions. Indeed these surfaces come in one-parameter families each of which includes a Smyth surface (with the umbilic removed) as a degenerate limit, in the same way that the Delaunay surfaces are a one-parameter family containing the sphere (with two points removed) as a degenerate limit. The next class consists of CMC cylinders which contain a closed planar geodesic. The third class presents cylinders each of which admits a closed curve of points with common tangent plane. Although it is very easy to read off the Hopf differential from the potential, it is usually unclear how the geometry of the surface is encoded in the potential. For example, there is as yet no understanding of the conditions on a potential which ensure that the surface is either proper, complete or embedded. The main obstacle in understanding the passage from the potential to the surface is a loop group factorization (the Iwasawa decomposition). This motivated us to build a numerical package which would compute this factorization and produce images of the surface: the approach is described below. The result is a computer laboratory called dpwlab written by the third author. Other attempts have been made to implement the DPW method numerically (e.g. [8]) but these find the Iwasawa decomposition by first turning it into a Riemann-Hilbert problem (i.e. Birkhoff factorization). The dpwlab directly computes the Iwasawa decomposition according to the theory described in [9]. Further Information. For further information about CMC surfaces, the DPW construction, and the dpwlab software, visit the Center for Geometry, Analysis, Numerics and Graphics website (www.gang.umass.edu) or write to the third author (nick@gang.umass.edu). Acknowledgments. We are grateful to Franz Pedit and Josef Dorfmeister for helpful discussions, and to Rob Kusner for his encouragement. This work was partially supported by NSF grants DMS-9626804, DMS-9704949 and DMS-9705479. The first author was also partially supported by SFB 288 at Technische Universität Berlin.
The DPW ConstructionBefore stating the DPW recipe, we introduce the ingredients. ForFurthermore, define 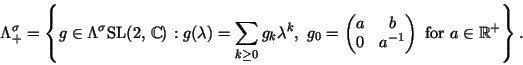
The principal tool in the DPW method is the loop group Iwasawa decomposition i.e. any
Now let us recall the DPW construction. Let D be a Riemann surface
and 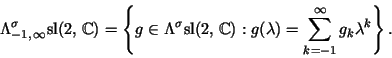
The following steps (cf. [5]) give an S1 family, called the associated family, of immersions (possibly with branch points)
We call the 1-form
We list here a number of properties of the construction which
will be relevant for our surfaces.
|
| |
(2) |
where p(z)=k zm, for
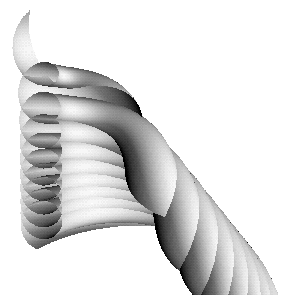 |
| Figure 1 Sector of a Smyth surface bounded by a nodoidal planar geodesics. |
More general surfaces can be obtained by allowing p(z) to be any
polynomial (cf. [5]). The resultant surfaces have m+2legs, where ![]() ,
each of which looks like a Smyth surface
leg. To the best of our knowledge, there has not been any work which
describes the strength of this resemblance. Of course, these surfaces
need not possess either intrinsic or extrinsic symmetries.
,
each of which looks like a Smyth surface
leg. To the best of our knowledge, there has not been any work which
describes the strength of this resemblance. Of course, these surfaces
need not possess either intrinsic or extrinsic symmetries.
Example 2. All the Delaunay surfaces can be obtained with the family of potentials
| |
(3) |
Here z is a coordinate on
| |
(4) |
transforms the potential (2) (on
Below we will use
![]() and
and
![]() to denote
respectively the holomorphic and unitary extended frames for the
potential
to denote
respectively the holomorphic and unitary extended frames for the
potential
![]() with
with
![]() .
In
particular, notice that
.
In
particular, notice that
![]() .
.
Remark. The Delaunay potentials fit into the following more general context. By a result of Burstall & Pedit [2, Thm 4.3], each CMC surface with doubly periodic Gauss map can be obtained from a holomorphic potential
There is a (g-2)-parameter family of CMC surfaces with the same spectral curve: for g=1 there is one surface for each spectral curve and this surface is a Delaunay surface. It can be shown (we omit the proof here) that one of the surfaces with the spectral curve above can be obtained by taking
where
Implementation of the DPW Procedure in Software
Of the three steps in the DPW process, the second step requires the most attention. The integration step 1 is performed using a standard fourth order Runge-Kutta method. We always work with potentials| |
(5) |
and define
The most time-expensive part of the software version of the DPW
procedure arises from computing the projections (5).
While these can be found directly (by e.g. the Gram-Schmidt
orthonormalization of the basis
![]() )
they are computed
more efficiently and stably with the following linear method.
If V is a finite-dimensional inner product space, U a subspace
with basis
)
they are computed
more efficiently and stably with the following linear method.
If V is a finite-dimensional inner product space, U a subspace
with basis
![]() ,
and
,
and ![]() ,
then
,
then
![]() where
where
![]() solve the
linear system
solve the
linear system
| |
(6) |
Since this system is Hermitian it can be solved by Cholesky decomposition. Notice that if
A further speedup is achieved when the twisted structure of the loop
group is exploited.
Two elements of
![]() with opposite polarity are
L2-orthogonal.
In this case, the linear system (6) decouples into two
simpler Hermitian systems.
This also means that the columns of
with opposite polarity are
L2-orthogonal.
In this case, the linear system (6) decouples into two
simpler Hermitian systems.
This also means that the columns of
![]() are already
orthogonal i.e.
are already
orthogonal i.e.
![]() is unitary. Hence the map
is unitary. Hence the map ![]() can be obtained by using
can be obtained by using
![]() in place of F in the
Sym-Bobenko formula and taking the trace-free part of the result.
in place of F in the
Sym-Bobenko formula and taking the trace-free part of the result.
CMC Cylinders
In this section we will present some new classes of CMC cylinderswhere we recall we have chosen to identify
is independent of w. However, we can prove the following crucial lemma.
Proof. Since
![]() we
have
we
have
![]() which implies
which implies
![]() .
The result now follows by uniqueness
of the Iwasawa decomposition.
.
The result now follows by uniqueness
of the Iwasawa decomposition.
Therefore, under the conditions of the lemma, we can sensibly call
![]() the holonomy of
the holonomy of ![]() (and in fact this implies
(and in fact this implies
![]() is periodic). Notice that if one knows that
the surface is a cylinder then
is periodic). Notice that if one knows that
the surface is a cylinder then ![]() necessarily has
well-defined holonomy. These observations allow us to formulate an
elementary characterization of the conditions under which a periodic
potential produces a periodic immersion.
necessarily has
well-defined holonomy. These observations allow us to formulate an
elementary characterization of the conditions under which a periodic
potential produces a periodic immersion.
iff the associated family member
We will usually work with
![]() .
Let us now consider some
classes of potentials which satisfy the conditions of this
proposition.
.
Let us now consider some
classes of potentials which satisfy the conditions of this
proposition.
Cylinders with One End Asymptotic to a Delaunay Surface
An interesting class of surfaces is obtained by perturbing the Delaunay potential (3) by a potential on
Proof. Consider the system (1) as a first order system of ODE with
a regular singular point at z=0. We will show below that a solution
![]() can be written in the form
can be written in the form
| |
(7) |
where
Now let us verify (7). For ![]() to exist, there must
be a solution to the differential equation
to exist, there must
be a solution to the differential equation
| |
(8) |
When we examine the expansion
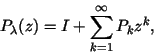
we discover we must have
Therefore the coefficients Pk can be recursively determined provided the operator
which is solved by
Notice that in this class of examples we have more or less complete freedom to specify the location of the umbilics.
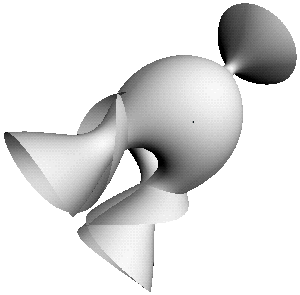 |
| Figure 2 CMC cylinder with two umbilics, one marked with a dot. Asymptotically, one end is a Delaunay nodoid with a thin neck and the other is a two-legged Smyth surface. Figure 3 shows a larger piece of this surface. |
Example 3. Let us begin by considering the simplest class of perturbations which produce unbranched surfaces with umbilics. Here we take
| |
(9) |
where q(z)=kzm for
| |
(10) |
which is (9) with a=1, b,c =0 and q(z)=-z2p(z). Therefore it makes sense to think of the surfaces we see as deformations of the Smyth surfaces, where the intrinsic S1-symmetry has been broken by the bifurcation of the multiple umbilic at z=0 into m umbilics at equal distance from the origin and at equal angles. Because of this, we conjecture that these cylinders are complete and proper immersions for which the end for

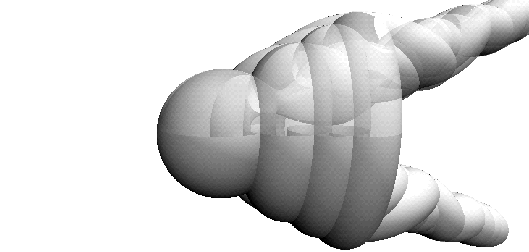
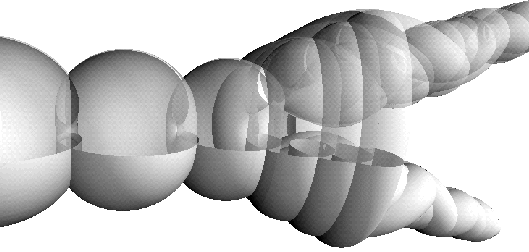 |
| Figure 3 Two-legged Smyth surfaces with Delaunay heads. The Smyth surface (middle) has a sphere-like head and is a singular boundary between the unduloidal and nodoidal examples. |
The m-fold rotational symmetry is explained by reference to the earlier discussion
2.1B. Let
![]() denote translation by
denote translation by ![]() .
This induces
on
.
This induces
on
![]() a rotation through this angle. Then
a rotation through this angle. Then
![]() ,
so the same is true for
,
so the same is true for
![]() .
A careful examination of the series
expansion of (8) shows that this implies
.
A careful examination of the series
expansion of (8) shows that this implies
![]() .
It follows that
.
It follows that
![]() belongs to
belongs to
![]() for w0=0, therefore we have all
the conditions for this symmetry to exhibit itself on the surface.
for w0=0, therefore we have all
the conditions for this symmetry to exhibit itself on the surface.
More general types of perturbations than (9) do not seem
to alter the end behavior a great deal. Certainly taking q(z) to be
any polynomial has the effect one expects from knowledge of the
generalized Smyth surfaces: the number of legs is ![]() and their
direction depends in some way upon the roots of q(z)-b. If we
consider perturbations at higher powers of
and their
direction depends in some way upon the roots of q(z)-b. If we
consider perturbations at higher powers of ![]() we can obtain
surfaces with no umbilics but they still appear to have the same end behaviour.
we can obtain
surfaces with no umbilics but they still appear to have the same end behaviour.
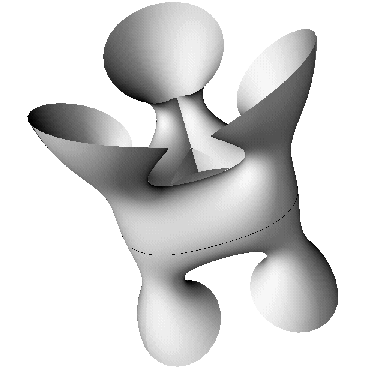
Example 4. The form of the potential (9) made us think that to some extent we may be able to treat holomorphic potentials like building blocks to patch two types of end behavior together. Therefore we considered potentials of the form
 |
| Figure 4 The double Mr. Bubble is two two-legged Smyth surfaces joined by an unduloidal neck. |
CMC Cylinders with a Closed Planar Geodesic
Proposition 3.2 gives conditions on the holonomy of
the extended unitary frame with
In the first class of potentials of this type we will also insist that
![]() both satisfy
both satisfy
![]() .
In this case, under the conditions of the next proposition, the image
of the unit circle is a planar geodesic: we exhibit some
examples in figure 7.
For the purposes of the next proposition, let z(t) denote the contour
.
In this case, under the conditions of the next proposition, the image
of the unit circle is a planar geodesic: we exhibit some
examples in figure 7.
For the purposes of the next proposition, let z(t) denote the contour
![]() in
in
![]() .
.
- 1.
-
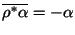 ,
,
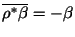 ;
;
- 2.
-
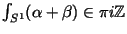 and
and
- 3.
-
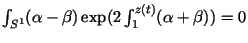 .
.
| |
(11) |
is the potential for a CMC cylinder with umbilics at the zeroes of
Proof. For ![]() ,
the solution of
,
the solution of
along
Since
Similarly, it is straightforward to check that the second holonomy condition of proposition 3.2 is implied by
where
Example 5. The simplest example is obtained with the forms
Here the constant
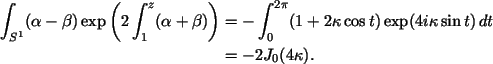
It follows that we have a discrete family of immersed CMC cylinders indexed by the zeroes of
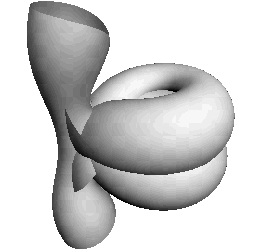
 |
| Figure 5 This CMC cylinder has the appearance of an unduloid conjoined with a nodoid. The figure-eight in the transparent image is the planar geodesic across which the surface has reflective symmetry. As it evolves toward an end, one of its loops sweeps out half of the unduloid, the other traces the opposite half-nodoid. |
More examples can be obtained using the following method. The first
holonomy condition is simply
![]() ,
where we consider
,
where we consider
![]() as 1-forms on
as 1-forms on ![]() with an isolated singularity at
z=0. For the second condition, set
with an isolated singularity at
z=0. For the second condition, set
![]() ,
then
,
then ![]() is a 1-form on
is a 1-form on
![]() by the first
holonomy condition. It is straightforward to show for any 1-form
by the first
holonomy condition. It is straightforward to show for any 1-form
![]() that
that
![]() whenever
whenever
![]() for
for
![]() with
with ![]() .
In particular we consider
the case where a is a primitive n-th root of unity. Then
.
In particular we consider
the case where a is a primitive n-th root of unity. Then
![]() ,
and the reality conditions are satisfied,
if
,
and the reality conditions are satisfied,
if
![]() are of the form
are of the form
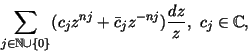
with
 ).
).
 |
| Figure 6 The planar geodesic of this CMC cylinder, marked in black, lies near the beginning of the sequence shown in figure 7. |
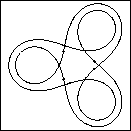
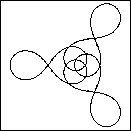
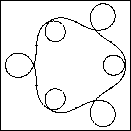
Figure 7 shows
a sequence of planar geodesic cross-sections for
CMC cylinders with potential (11) for
![]() and
and
![]() ,
where
,
where
![]() .
For c=0 we obtain the round sphere. As c increases (left to right)
the curves acquire more loops.
.
For c=0 we obtain the round sphere. As c increases (left to right)
the curves acquire more loops.




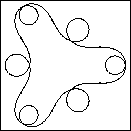 |
| Figure 7 Planar geodesics which are the cross sections of a CMC cylinder family. The dots mark the six umbilic points. |
Other CMC Cylinders
Another class of examples is obtained by asking that the holomorphic
potential satisfy the conditions
| |
(12) |
is the potential for a CMC cylinder with umbilics at the zeroes of
Proof. Since
![]() ,
the solution
,
the solution
![]() to (1)
with
to (1)
with
![]() has
has ![]() .
As above,
.
As above,
![]() over the unit circle and we deduce
over the unit circle and we deduce
![]() ,
so the first holonomy condition of proposition
3.2 is satisfied. The second holonomy condition
follows from
,
so the first holonomy condition of proposition
3.2 is satisfied. The second holonomy condition
follows from
as in the proof of proposition 3.4.
The cylinders generated by these potentials have constant frame
![]() over the unit circle. This means that the Gauss map is
constant along the image of the unit circle so that this lies on a
single tangent plane to the surface.
over the unit circle. This means that the Gauss map is
constant along the image of the unit circle so that this lies on a
single tangent plane to the surface.
Example 6. First, this class contains all Delaunay nodoids. These arise if we take any
achieved by gauging the left-hand potential by
where z=ew. This left-hand potential is
By contrast, if we take
![]() we obtain the surface in
figure 8. This example displays
the characteristic features of the cylinders in this class.
we obtain the surface in
figure 8. This example displays
the characteristic features of the cylinders in this class.

 |
| Figure 8 This CMC cylinder is tangent to a plane along the black curve in solid figure. |
More generally, if
![]() for a polynomial p(z), we have observed that
the resulting surface has
for a polynomial p(z), we have observed that
the resulting surface has ![]() legs emerging within a
nodoid-like sheath. Experiments suggest that all surfaces in this
class are bounded by the outer nodoid-like surface.
legs emerging within a
nodoid-like sheath. Experiments suggest that all surfaces in this
class are bounded by the outer nodoid-like surface.
Concluding Remarks
It is difficult to convey in static pictures the intuition gained by being able to rotate, cut away and zoom in on these surfaces. One feature which struck us was the ubiquity of nodoidal and unduloidal features in the ends. In fact, the Smyth end itself, which at first looks impossibly complicated, appears to have the following simple description. Consider the 2-legged Smyth end. Divide the region |z| >1 into its four quadrants. The lines at angles
The surfaces introduced in sections
3.2 and 3.3 have a similar description
as we rotate around
![]() .
But their behaviour as the radius
increases or decreases is quite different. From the figures 5 and 8 we are
lead to ask: are either of these surfaces bounded by a standard cylinder?
.
But their behaviour as the radius
increases or decreases is quite different. From the figures 5 and 8 we are
lead to ask: are either of these surfaces bounded by a standard cylinder?
For the surface with a planar geodesic in figure 5, as |z| increases from |z|=1 (or as it decreases) each circle is stretched in two opposite directions in 3-space. Since the image of circles of constant |z| appear to pass through the central plane of reflection not far from the planar curve, it is not yet settled whether these examples are properly immersed.
On the other hand, the surface in figure 8 seems to be made by translating the same shape as the radius |z| increases and decreases from |z|, although this cannot be literally true since there is only one umbilic (and branch point): it lies at z=-1. This suggests that this map is proper.
It seems that these surfaces give two new types of end behaviour which, although they are immersed, do not appear to be significantly more complicated than the Smyth surfaces.
Bibliography
-
- 1
- A Bobenko,
Constant mean curvature surfaces and integrable equations,
Russian Math. Surveys 46 (1991), 1-45.
- 2
- F E Burstall & F Pedit,
Harmonic maps via Adler-Kostant-Symes theory, in
Harmonic maps and integrable systems,
ed: A P Fordy & J C Wood, Aspects of Mathematics E23, Vieweg 1994.
- 3
- F E Burstall & F Pedit,
Dressing orbits of harmonic maps,
Duke Math. J. 80 (1995), 353-382.
- 4
- J Dorfmeister & G Haak, Constuction of non-simply
connected CMC surfaces via dressing, preprint, SFB 288, TU Berlin.
- 5
- J Dorfmeister, F Pedit & H Wu,
Weierstrass type representation of harmonic maps into symmetric spaces,
Comm. Anal. Geom. 6 (1998), 633-668.
- 6
- J Dorfmeister & H Wu,
Constant mean curvature surfaces and loop groups,
J. Reine Angew. Math. 440 (1993), 1-47.
- 7
- N Korevaar, R Kusner & B Solomon,
The structure of complete embedded surfaces with
constant mean curvature, J. Diff. Geom. 30 (1989), 465-503.
- 8
- D Lerner & I Sterling,
Construction of constant mean curvature surfaces using the DPW
representation of harmonic maps, SFB 288 Preprint no. 92 (1993),
Technische Univ. Berlin.
- 9
- A Pressley & G Segal,
Loop groups, Oxford Mathematical Monographs, OUP, Oxford, 1986.
- 10
- B Smyth,
A generalization of a theorem of Delaunay on constant mean
curvature surfaces, in
Statistical thermodynamics and differential geometry of
microstructured materials,
123-130, IMA Vol. Math. Appl. 51 Springer, New York 1993.
- 11
- I Sterling & H Wente,
Existence and classification of constant mean curvature
multibubbletons of finite and infinite type,
Indiana Univ. Math. J. 42 (1993), 1239-1266.
- 12
- M Timmreck, U Pinkall & D Ferus,
Constant mean curvature planes with inner rotational
symmetry in Euclidean 3-space, Math. Z. 215 (1994), 561-568.