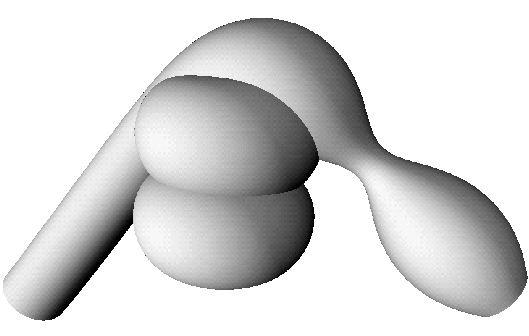New Constant Mean Curvature Trinoids
N. Schmitt
August 23, 1999
Abstract
I construct two families of constant mean
curvature genus-zero
surfaces with three ends via the DPW construction.
One of these families is known and has three unduloid ends;
the other is a new family with two unduloid and one nodoid
end.
The classification of the
almost-embedded CMC genus-zero surfaces with three ends
-- the trinoids with unduloid ends, or triunduloids --
was announced by
Große-Brauckmann, Kusner, and Sullivan [2].
In this note, I construct these examples explicitly
(result 1)
using a method due to Dorfmeister, Pedit and Wu [1],
and present a new family of CMC trinoids
(result 2)
which enjoy two unduloid and one nodoid end.
Taking H>0 to be a fixed mean curvature,
the space of triunduloids may be described as follows.
Result 1
Let
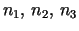
be real numbers in the interval
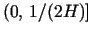 satisfying
Then there exist two potentials which,
with appropriate initial conditions,
produce trinoids with
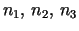
as neck radii,
except when any of the above four inequalities is an
equality; in this case there is exactly one such trinoid.
We extend this result to trinoids with two unduloid and and one nodoid end
(that is, ends asymptotic to Delaunay unduloids and nodoids respectively).
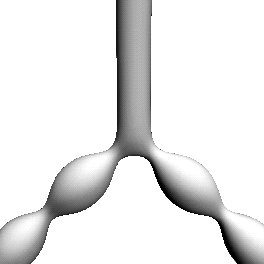
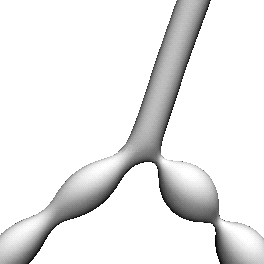
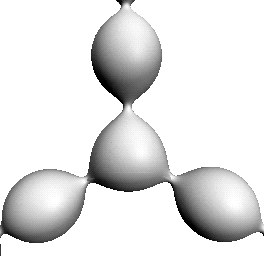
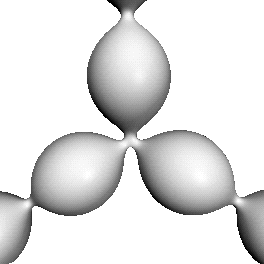
Figure:
These CMC triunduloids lie in the one-parameter
family whose neck radius sum is maximal. Each of the isosceles and
scalene examples has a cylindrical end.

 |
Result 2
Let
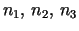
be real numbers in the intervals
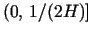 ,
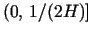 ,
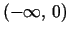
respectively
satisfying
Suppose further that the end weights
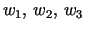
corresponding
to the neck radii
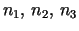
satisfy
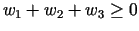 .
Then there exist two potentials which, with appropriate
initial conditions, produce trinoids with
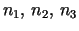
as neck radii,
except when any of the above three inequalities
for
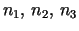
is an equality;
in this case there is one such trinoid.
These surfaces were produced with two tools I developed at the
Center for Geometry, Analysis, Numerics and Graphics (GANG).
The algorithm for the main software, DPWLab,
which computes CMC surfaces from DPW potentials, is discussed in [1].
The second tool, killerB, discussed in more detail below,
uses an unsophisticated but very stable algorithm to compute the
initial condition for which a surface simultaneously closes at its ends.
Figure:
The top images show equilateral trinoids with
equal neck radii but opposite phase; the one
joined at a central bulge, the other meeting in a thin neck.
The lower image is a cutaway view of an equilateral trinoid whose neck
radii are so small that it self-intersects.
 |
Neck Radii and End Weights.
The minimum and maximum radii 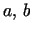 of a Delaunay unduloid
satisfy
0<a<1/(2H)<b<1/H, with constant sum a+b=1/H.
It is natural to extend this notion of neck and bulge radii
to the round cylinder
(
a=b=1/(2H)), the round sphere (
of a Delaunay unduloid
satisfy
0<a<1/(2H)<b<1/H, with constant sum a+b=1/H.
It is natural to extend this notion of neck and bulge radii
to the round cylinder
(
a=b=1/(2H)), the round sphere (
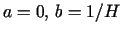 ), and
to the nodoid, where a<0<1/H<b.
In all cases, the sum is a+b=1/H. ), and
to the nodoid, where a<0<1/H<b.
In all cases, the sum is a+b=1/H.
The end weight, defined as w=ab,
is at most 1/(4H) (for the round cylinder)
and like the neck radius, is positive for unduloids,
zero for the round sphere, and negative for nodoids.
The Family of Trinoid Potentials.
The family of DPW potentials generating the trinoids of results
1 and 2 are meromorphic on
the thrice-punctured Riemann sphere and are asymptotic to
the DPW potential for a Delaunay surface at each puncture.
For
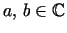 and
and
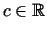 I denote this potential by I denote this potential by
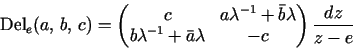 |
(1) |
The Delaunay surface produced by this potential is closed if
and only if 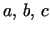 satisfy
satisfy
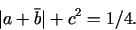 |
(2) |
Fix distinct points
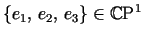 .
The space of trinoid potentials is parameterized by .
The space of trinoid potentials is parameterized by
as follows.
Fix
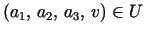 and let
s=a1+a2+a3.
Let
and let
s=a1+a2+a3.
Let
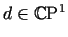 satisfy
satisfy
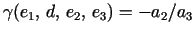 .
Here, .
Here, 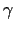 denotes the cross ratio
denotes the cross ratio
Then the trinoid potential
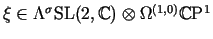 is the unique form with divisor
-[e1]-[e1]-[e3]-[d]and residues is the unique form with divisor
-[e1]-[e1]-[e3]-[d]and residues
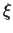 is the potential for a (closed) constant mean curvature immersion
is the potential for a (closed) constant mean curvature immersion
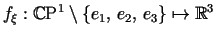 under the DPW procedure for initial condition found numerically.
The resulting trinoid will be denoted under the DPW procedure for initial condition found numerically.
The resulting trinoid will be denoted 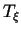 . .
Figure:
Two views of an isosceles CMC trinoid with one nodoid end;
all three ends extend infinitely downward.
In contrast to the triunduloids, the two umbilic points lie
not symmetrically about the mirror plane but on it.

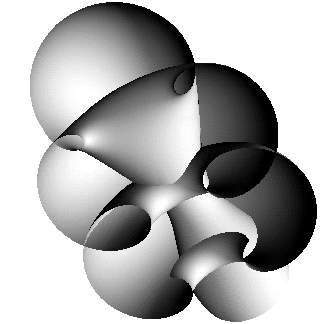 |
The Parameter Space Conditions.
Of the two conditions defining U,
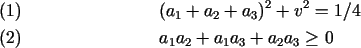
(3) insures that at each of its poles
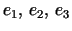 ,
the Delaunay potential (1)
to which ,
the Delaunay potential (1)
to which 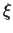 is asymptotic satisfies the
closing condition (2).
is asymptotic satisfies the
closing condition (2).
The remaining condition (4) defining Uarises from a balancing formula [3]
according to which the sum of the forces exerted by each end
is zero. It follows that the end weights must satisfy the
inequality
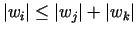 for each permutation
for each permutation 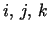 of of
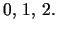
Each trinoid 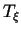 is represented several times in Ubecause (a) permutations of the parameters
is represented several times in Ubecause (a) permutations of the parameters
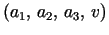 produce the same trinoid with
ends permuted, and (b)
produce the same trinoid with
ends permuted, and (b)
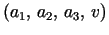 and
and
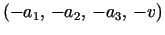 trivially produce the same surface. trivially produce the same surface.
On the other hand, there are
two trinoids for each choice of neck radii unless v=0.
The two values 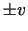 give
two triunduloids with identical neck radii but opposite phase:
one has a bulge in the middle, and the other a neck. This
phenomenon is illustrated in figures
1 and 5.
give
two triunduloids with identical neck radii but opposite phase:
one has a bulge in the middle, and the other a neck. This
phenomenon is illustrated in figures
1 and 5.
End Types.
The family of trinoids parametrized by 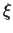 must have either
(a) three unduloid ends, or (b) two unduloid and one nodoid end.
Trinoids with more than one nodoid end cannot arise in this
family.
To see this, note that
the ends
must have either
(a) three unduloid ends, or (b) two unduloid and one nodoid end.
Trinoids with more than one nodoid end cannot arise in this
family.
To see this, note that
the ends
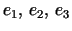 are unduloidal or nodoidal according as
their weights
4a1(a2+a3),
4a2(a1+a3),
4a3(a1+a2) are
positive or negative respectively.
Because are unduloidal or nodoidal according as
their weights
4a1(a2+a3),
4a2(a1+a3),
4a3(a1+a2) are
positive or negative respectively.
Because
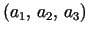 and
and
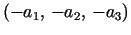 give the same trinoid, as do
permutations of
give the same trinoid, as do
permutations of
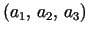 ,
without loss of generality there are two cases:
(a) a1>0, a2>0, a3>0, and (b) a1>0, a2>0, a3<0.
Case (b) yields a trinoid three unduloid ends.
In case (b),
a3(a1+a2)<0, making e3 unduloidal.
The condition
a1 a2 + a1 a3 + a2 a3 > 0means that
a1(a2+a3) > -a2 a3 and
a2(a1+a3) > -a1 a3.
But
-a2 a3 > 0, so
a1(a2+a3) > -a2 a3 > 0, and likewise
-a1 a3 > 0, so
a2(a1+a3) > -a1 a3 > 0.
Hence each of the remaining two ends are unduloidal. ,
without loss of generality there are two cases:
(a) a1>0, a2>0, a3>0, and (b) a1>0, a2>0, a3<0.
Case (b) yields a trinoid three unduloid ends.
In case (b),
a3(a1+a2)<0, making e3 unduloidal.
The condition
a1 a2 + a1 a3 + a2 a3 > 0means that
a1(a2+a3) > -a2 a3 and
a2(a1+a3) > -a1 a3.
But
-a2 a3 > 0, so
a1(a2+a3) > -a2 a3 > 0, and likewise
-a1 a3 > 0, so
a2(a1+a3) > -a1 a3 > 0.
Hence each of the remaining two ends are unduloidal.
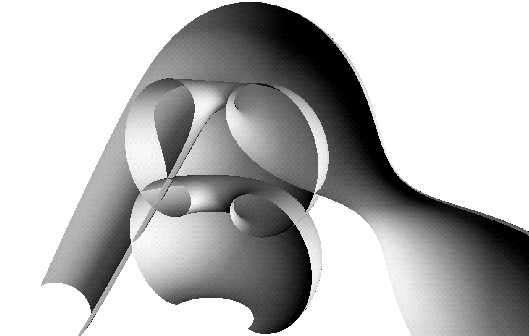
Figure:
This CMC trinoid has three ends which are asymptotically a cylinder,
a nodoid, and an unduloid.
The three downward ends have zero-sum force because the nodoid
end's force is upward.
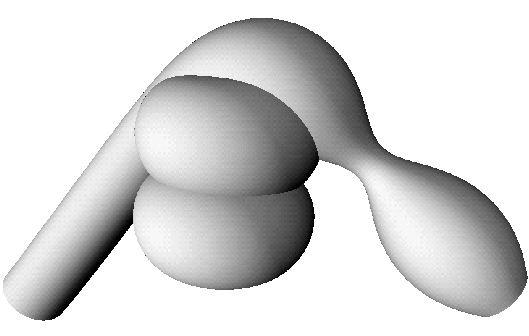
 |
Asymptotics.
At each of its poles
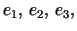 the z-leading-order term of the z-leading-order term of  is the DPW potential for a closed Delaunay surface Di,
and the trinoid is the DPW potential for a closed Delaunay surface Di,
and the trinoid  converges to Di near ei.
converges to Di near ei.
Near e1, 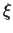 is a is a special perturbation of a Delaunay surface
in which the leading-order z-term of
is a is a special perturbation of a Delaunay surface
in which the leading-order z-term of
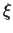 commutes with its holomorphic part. This means that there is
a linear space of initial conditions for which the CMC immersion
closes (has trivial holonomy) at this end.
commutes with its holomorphic part. This means that there is
a linear space of initial conditions for which the CMC immersion
closes (has trivial holonomy) at this end.
Cone Points.
The point
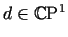 ,
while a simple pole of ,
while a simple pole of 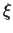 ,
is
a regular point for the resulting immersion.
Writing ,
is
a regular point for the resulting immersion.
Writing
the cross-ratio condition for d guarantees that
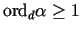 ,
so the Hopf form has no pole
at d. ,
so the Hopf form has no pole
at d.
Symmetry.
If
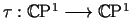 is the anticonformal diffeomorphism
fixing
is the anticonformal diffeomorphism
fixing
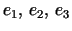 ,
then ,
then
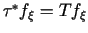 for a
reflection R of
for a
reflection R of
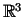 .
Hence each trinoid .
Hence each trinoid 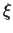 has
a plane of reflective symmetry.
has
a plane of reflective symmetry.
Figure:
These two isosceles trinoids with one nodoid end
are sliced through a mirror plane. As with the triunduloids
in figure 2 they have correspondingly equal
neck radii and opposite phase.
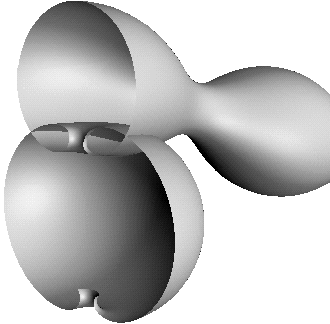
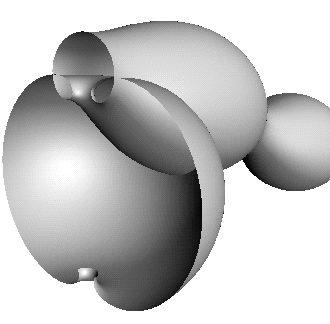 |
Umbilics.
Each trinoid 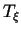 has two umbilic points,
whose preimages
has two umbilic points,
whose preimages
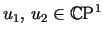 are the zeros of the coefficient
of
are the zeros of the coefficient
of
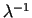 in the lower-right entry of
in the lower-right entry of 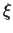 .
For triunduloids .
For triunduloids 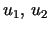 are interchanged by the involution
are interchanged by the involution
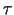 and hence by the reflection
and hence by the reflection 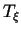 of
of
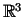 .
For trinoids with one nodoid end, .
For trinoids with one nodoid end, 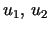 are individually
fixed by
are individually
fixed by 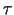 and lie in the plane of reflective symmetry of
the trinoid.
and lie in the plane of reflective symmetry of
the trinoid.
Period Closing.
As the DPW potentials for these surfaces became clear,
I implemented period-closing software killerB
to solve the holonomy problem numerically and verify that the potentials
indeed produce trinoids.
Since the desired initial condition is not a constant but a
loop group element, the period closer's search space is an
infinite dimensional space of Fourier series,
so for the purposes of computation it is necessary to restrict
to a finite dimensional subspace by truncating the series.
The period-closing software uses a brute-force algorithm.
Starting with an arbitrary initial guess, it cycles through
the dimensions of the search space (the loop group coefficients),
varying one parameter at a time while holding the others fixed.
In this way it minimizes, one dimension at a time, an error measure
of the holonomy by quadratic interpolation.
By stair-stepping through the parameters, the algorithm slowly
converges to a stable relative minimum which in practice is
the global minimum.
It is interesting to note that the periods of ends with small neck
radii converge much more quickly than do those near the maximal limit.
As noted above, due to the special structure of the potential,
at one end a linear space of initial conditions can be found for
which the trinoid closes.
Within this space, the period-closing software must be used
to close a second end. Because the holonomy around the third end
coincides with the composition of holonomies around the other two,
the closing condition on the third end is vacuous.
Acknowledgments. I thank
Ian McIntosh, Martin Kilian, and Rob Kusner.
This work was partially supported by NSF grants DMS-9626804 and
DMS-9704949.
Bibliography
-
- [1]
-
J Dorfmeister, F Pedit & H Wu,
Weierstrass type representation of harmonic maps into symmetric spaces,
Comm. Anal. Geom. 6 (1998), 633-668.
- [2]
-
K Große-Brauckmann, J Sullivan & R Kusner,
Constant Mean Curvature Surfaces with Three Ends,
Proc. Nat. Acad. Sci. [in press].
- [3]
-
R Kusner,
Bubbles, Conservation Laws, and Balanced Diagrams,
Geometric Analysis and Computer Graphics,
MSRI Publications 17 1991 103-108.
Center for Geometry, Analysis, Numerics and Graphics
Dept. of Mathematics
University of Massachusetts
Amherst, MA 01003, USA.
nick@math.umass.edu
|