Undergraduate Research at GANG Summer 2000 Curves and Immersions  The Flower Sequence 1 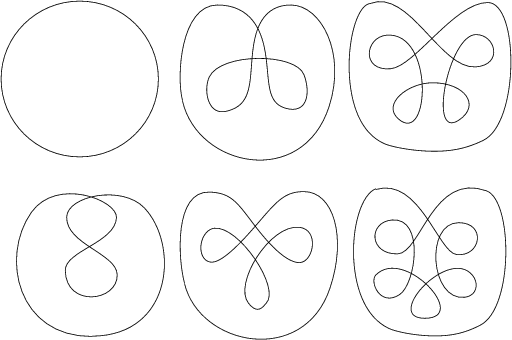The sequence takes a curve with a single inner loop and adds successive outer loops that (inner) loop. The curves in the top row bound nothing. The curves on the bottom bound successively higher genus manifolds. That is, the first bounds a punctured sphere (a disk), the second a punctured torus the third a punctured two-torus. The sequence continues in this manner. If one considers the curves on the bottom with 1 added to each degree number, not only do these curves bound n-tori but also (n-1)-tori in multiple ways. The number of immersions (an) increases as n increases according to the sequence an = 4 an-1-1.