Imagine a clear sky on a moonless night in a place like Amherst. Being mathematicians, we ignore the few thousand nearby stars and the faint glow of our Milky Way or other nearby galaxies. What remains is the uniformly dark background, which any of us can observe directly. This basic observation supports a cosmic hypothesis: on a large scale, we live in a space which looks the same in all directions and the same at all points and which is locally like the up-down, front-back, left-right world of everyday experience. In more mathematical terms, our present universe can be modeled by an isotropic and homogeneous three-manifold.
What are the consequences of this mathematical model of the cosmos? The first is that such a manifold has constant curvature. This means that the laws of trigonometry are the familiar ones from Euclidean (flat, or zero-curvature) geometry, or their spherical (positive-curvature) or hyperbolic (negative-curvature) counterparts. We could even measure this curvature experimentally. Indeed, if we are only interested in the sign of the curvature, the experiment is very simple: construct a triangle in space with straight (geodesic) edges and add up the vertex angles; when the angle sum is exactly 180 degrees, space is flat; otherwise, space is positively or negatively curved when this angle sum is greater or less than 180 degrees, respectively. The great German mathematician C. F. Gauss carried out this experiment and found, within the precision of his early 19th century instruments, that space appeared to be flat. This is a rather famous result: both Gauss and his experiment were depicted on the last series of 10-mark notes in Germany before the euro became the currency there.
By the turn of the 20th century, mathematicians like H. Poincare, F. Klein, and D. Hilbert had become interested in classifying these three-manifolds, both as cosmological models and for their independent mathematical interest. Of particular importance are the closed three-manifolds of constant curvature; these manifolds have no boundary but are of finite extent. The simplest example is the round three-sphere, which has positive curvature. This can be thought of as the unit-length vectors in four-dimensional space, but another useful way to visualize the three-sphere is as a three-ball with all of its boundary identified to a single point.
Another example of a closed three-manifold of constant curvature is the three-torus. This is a flat three-manifold obtained by gluing the top and bottom, front and back, and left and right faces of a cube, like a cosmic version of the Mario Brothers video game; this space parametrizes the configurations of a carpenter's folding ruler with four segments and three pivots (the typical ruler with a dozen segments and eleven pivots corresponds to an eleven-torus)! Even if you've never played with a carpenter's ruler you can imagine something of what life would be like if the universe were shaped like a three-torus. If you were to stand in a three-torus and shine a flashlight straight ahead, instead of disappearing into darkness the light would illuminate the back of your head! This is because the light leaves the front face of the cube and re-enters the back face, which was glued to the front to form the three-torus. Similarly shining the light down at your feet would reveal the top of your head, and shining the light to the right would light up your left side (hopefully your good side). The effect is something like being in a completely mirrored room, except that instead of your reflected image you see a parallel translation of yourself. The three-torus is a fairly complicated three-manifold, but over the last hundred years topologists busily manufactured even more exotic examples. For instance, instead of a cube, take a solid dodecahedron. This is the famous geometric object from antiquity with 12 pentagonal faces that forms the basic structure underlying a soccer ball. Glue the opposite faces of a dodecahedron together in pairs by twisting each 18 degrees clockwise (you might need a rather stretchy dodecahedron for this). This yields a three-manifold of positive curvature originally discovered by Poincare and today called the Poincare dodecahedral space in his honor.
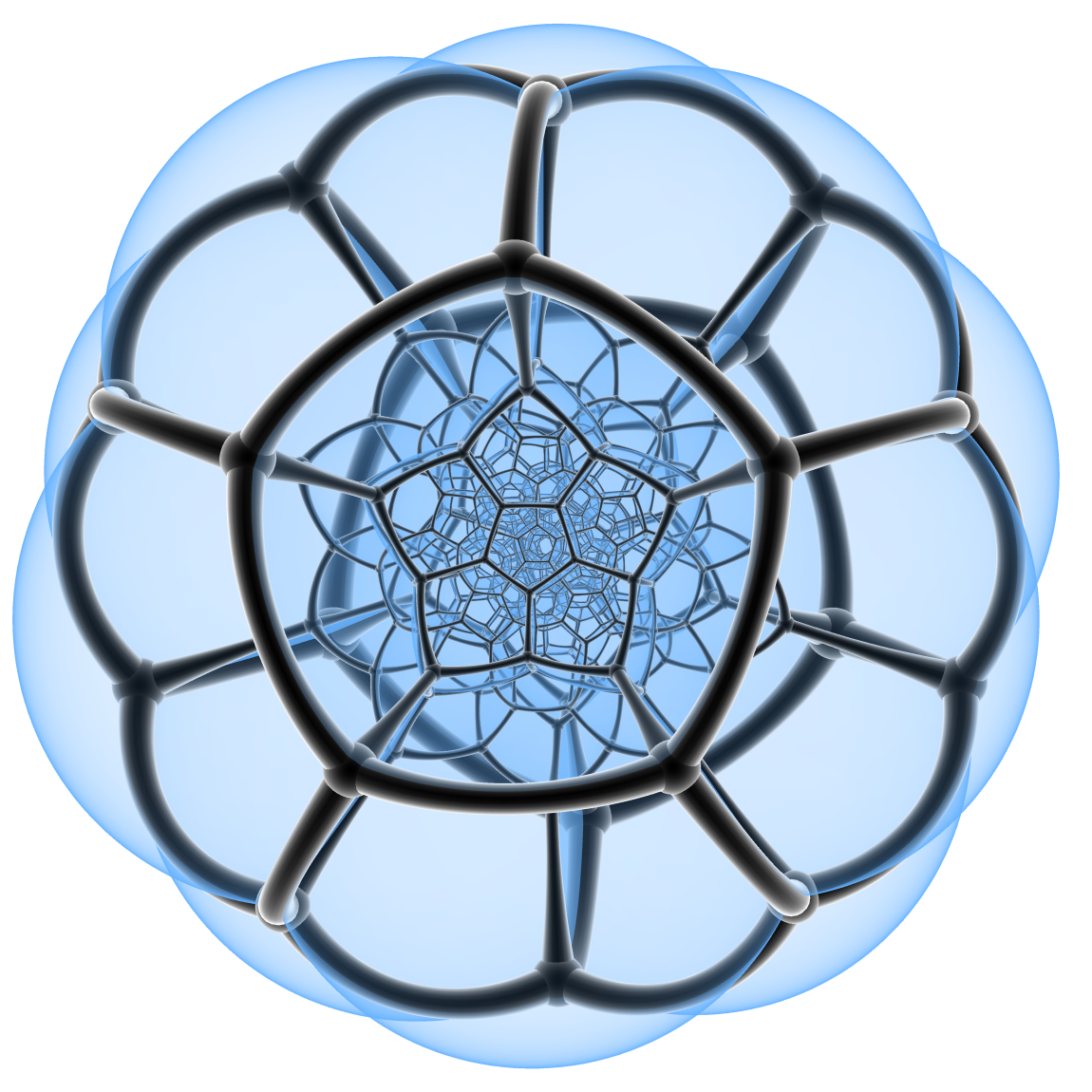 This figure shows something of what this
space looks like, although it's hard to draw in our mundane three-
dimensional world. The dodecahedral space has the remarkable property
that every loop bounds a surface, although actually proving this
requires some delicate algebra. Indeed, at first Poincare thought
this space was a counterexample to his conjecture.
This figure shows something of what this
space looks like, although it's hard to draw in our mundane three-
dimensional world. The dodecahedral space has the remarkable property
that every loop bounds a surface, although actually proving this
requires some delicate algebra. Indeed, at first Poincare thought
this space was a counterexample to his conjecture.
Around the same time, and with some friendly competition from Poincare and Hilbert, A. Einstein had the revolutionary idea that space is not static but dynamic, and that its geometry or metric evolves by a wave equation that now bears his name. Although the Einstein equation in general remains difficult to understand mathematically, special cases have been solved when the space-like slices are three-manifolds of constant curvature. For example, the deSitter model, where all the slices are three-spheres of time-varying constant curvature, is currently employed to explain the observed Hubble expansion of the universe.
As typical of the long, give-and-take tradition between physics and geometry, mathematicians began to use this new physical intuition to conjecture and prove results about the geometry and topology of manifolds with natural curvature-conditions. For example, in Einstein's theory, positive energy-density translates into a positivity condition on curvature, and the Ricci curvature in particular. This led to one thread of research, starting in the 1930s, when S. Bochner and A. Lichnerowicz showed that Ricci curvature is closely related to the topology of a closed manifold (positive Ricci curvature implies the vanishing of the first homology, for example). Around 1940 S. Myers proved that positive Ricci curvature implies finite fundamental group (the more refined algebraic structure invented by Poincare when he realized that homology alone could not distinguish the three-sphere from the dodecahedral-space). In fact, Myers observed that Ricci curvature is enough to control the average focusing of geodesics, an argument that inspired the much more recent singularity theorems of R. Penrose and S. Hawking in general relativity. By the 1970s my advisor R. Schoen, along with L. Simon, S. T. Yau, and my colleague and collaborator Bill Meeks had taken up minimal surface methods (instead of using geodesics) to generalize many of these ideas to manifolds of positive scalar curvature. And perhaps the culmination of this thread of work, with important feedback into physics, has been the proofs of the Positive Mass Theorem and more recently the Penrose Inequality by Schoen, Yau, and their students.
Another thread leads rather directly from Einstein's ideas of cosmological evolution to the geometric ideas that were developed by R. Hamilton and G. Perelman to solve the Poincare and Geometrization Conjectures. To get a flavor of this, we return to the period just before 1920 when Hilbert had realized that the equations of general relativity were of a variational nature: criticality for the total scalar curvature functional (perhaps with a volume constraint) gives rise to the Einstein equations for the geometry. Thus a natural way to get a nice geometry on a three-manifold might be to use the direct method in the calculus of variations to find such critical metrics. This approach was attempted by H. Yamabe in 1950s, but it is quite subtle since the critical metrics are infinitely unstable: along conformal changes of metric one can minimize the total scalar curvature functional (this became known as the Yamabe problem, solved by Schoen in the early 1980s), but in transverse directions one must maximize this functional to achieve an Einstein metric, which on a three-manifold is a metric of constant curvature. This maximization problem has not yet been solved, although M. Anderson obtained some partial results in that direction about a decade ago.
What was Hamilton's successful approach? Instead of focusing on the critical metric itself, he studied the dynamical flow that would evolve to such a critical metric. And his key insight, based on years of experience with the heat flow for harmonic maps, was to replace the Einstein wave equation with an analogous heat equation for the metric, known as the Ricci flow, which treats the curvature like a molten material to be equitably redistributed around the manifold. Hamilton's first result in the early 1980s recovered the theorem of Myers as a special case, at least in dimension three: when the Ricci curvature is positive, the Ricci flow evolves a metric on a three-manifold to one of constant positive curvature, like that on the three-sphere or the dodecahedral space.
Later in the 1980s, Hamilton, spurred on by Yau, began in earnest to apply his Ricci-low methods to study the three-dimensional Poincare Conjecture as well as the more general Geometrization Conjecture for three-manifolds made in the 1970s by W. Thurston. This conjecture is a natural outgrowth of the ideas from the time of Poincare, Klein, Hilbert, and Einstein, asserting that any three-manifold can be decomposed into pieces that carry either a constant-curvature geometry (recall that means homogeneous and isotropic), or else a slightly less symmetric geometry that is merely homogeneous. There are five additional types of the latter geometry. Although explaining all this in detail would, to borrow a line from Poincare, "take us too far away," in effect what Hamilton began to realize (and what Perelman perfected) was that while the constant curvature geometries arise as steady states of the Ricci flow, the other five homogeneous geometries arise naturally where the dynamics of the Ricci flow is more complicated and where topological changes (neck pinching or surgery: physicists might call these "wormholes") happen. This picture is not yet completely clear, even to the experts, so this is probably a good place to stop....
