Theory

For any conformal map X from C to IR^3 ${\rm I\!R^2\hspace{1mm}}$, $\Delta X=2\lambda^2 H\times N$ where

$$\lambda=<\frac{\partial}{\partial x}X,\frac{\partial}{\partial x}X>,$$

H is the mean curvature, and N is the normal vector. We now define U as the mean curvature half density of the surface, equal to $\lambda*H$. We can obtain a conformal map by taking two arbitrary holomorphic functions of x and y, $\psi_1$ and $\psi_2$, and plugging them into the formula:

$$\begin{eqnarray*}X_1 &=& \int_{x_0,y_0}^{x,y} \frac i2 * (\bar{\psi_2}^2 + \psi_... ..._0}^{x,y} \bar{\psi_2} \psi_1 dz + \psi_2 \bar{\psi_1} d\bar{z} \end{eqnarray*}$$

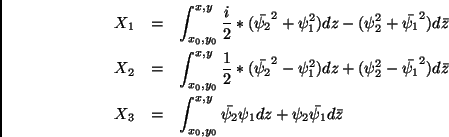
We now assume that $\psi_1$ and $\psi_2$ satisfy the differential equations:

  

$$\frac{d}{dz}\psi_2 + U*\psi_1$$ = 0 (1)

$$- \frac{d}{d\bar{z}}\psi_1 + U*\psi_2$$ = 0 (2)

If we assume $\psi_1$ and $\psi_2$ are of the form:

  

$$\psi_1$$ = h₁(x)*e^iy (3)

$$\psi_2$$ = h₂(x)*e^iy (4)

(1) and (2) can be rewritten in terms of h₁ and h₂ as follows:

  

h₁' = 2U*h₂ + h₁ (5)

h₂' = -2U*h₁ - h₂ (6)

Using (1)-(6), we obtain a surface of revolution as follows:

$$\begin{eqnarray*}X_1 &=& \sin{2y_0} \int_{x_0,y_0}^{x,y_0} (h_2^2-h_1^2) dx + \f... ...{2y_0} + \cos{2y}) \\ X_3 &=& 2 \int_{x_0,y_0}^{x,y_0} h_1 h_2 \end{eqnarray*}$$

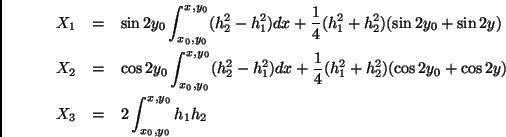
We have the differential equations (5) and (6) satisfied by h₁ and h₂:

$$\sin2y \int_{x_0,y_0}^{x,y_0} (h_2^2-h_1^2) dx = -(h_1^2+h_2^2) * \frac14 \sin{2y_0}$$

So:

$$X = \left\{ \begin{array}{l} (\sin{2y}) (h_1^2 + h_2^2) / 4 \... ...}) (h_1^2 + h_2^2) / 4 \\ \int 2 h_1 h_2 \end{array} \right.$$

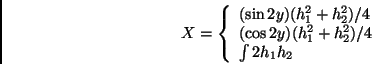
As a result, the parametrization is a surface of revolution.

Thus, given the mean curvature half density of a surface, U, we can solve the differential equations and obtain a parametrization for a surface of revolution.