*if the proportions of this page seem off, try refreshing.

Weeks (-Infinity,0)

Recall that in ordinary differential equations (ODEs) we study how systems evolve if we specify initial conditions and/or boundary values. These are useful in studying natural phenomena as well as theoretical hypotheses. Qualitatively we can study the general behavior of solutions given varying initial conditions. Numerically or analytically, we can solve systems of ordinary differential equations.

The study of partial differential equations (PDEs) is similar to that of ODEs. In both cases, we specify initial conditions and watch the evolution throughout time. The distinction lies in the use of partial derivatives of multiple variables as opposed to full derivatives of a single variable. In our study the partial derivates are taken with respect to space and time, x and t. Changes of coordinates are often made to simplify and decouple the systems of PDEs.

Many introductory physics textbooks define a wave as a disturbance that transports matter or energy. These disturbances are ubiquitous in science and are the focus of our study. Waves can be studied mathematically. They arise in the solutions of differential equations. Waves have many manifestations depending on how the system is interpreted.

While we study many different physical and non-physical systems, each of these systems has the same basic template. Ut+F(U)x=0 (subscripts are partial derivatives). This is called the “conservation form” of a conservation law. If U is a scalar then it is called the “state variable”. If U is a vector then the components of U are the state variables. F is called the "flux function".

One of the fundamental concepts in our research is to examine the evolution of a state variable in space through time, or in spacetime. Waves are shown below in what is called the “phase plane”. The vertical coordinate is time (t); the horizontal, space (x). The state variable is implicitly a third dimension.

The lines shown above are “characteristic curves”. Characteristics are defined so that the state variable is constant on the curve. They are analogous to level curves of three dimensional graphs. They are the fixed point solutions of a series of ordinary differential equations. The places where the lines fan out as t increases are called "rarefractions." The places where the lines converge are called "compressions."

In the scalar case we rewrite our template as Ut+Fu*Ux=0. This is called “quasi-linear form.” We imagine a curve C in the phase plane whose derivative with respect to time is equal to Fu. Integrating and noting that Fu is constant with respect to time we find that C-Cinitial=Fu*t

Using this result, we can make the computer draw each characteristic separately and recombine them to form the above pictures. See the Characteristic Plotter program.

Another way to examine a wave is to look at profiles in time. We start with an initial profile and specify the differential equation that the system obeys. The profile changes as time passes. When the system is “linear,” the profile shifts undistorted at a fixed speed.

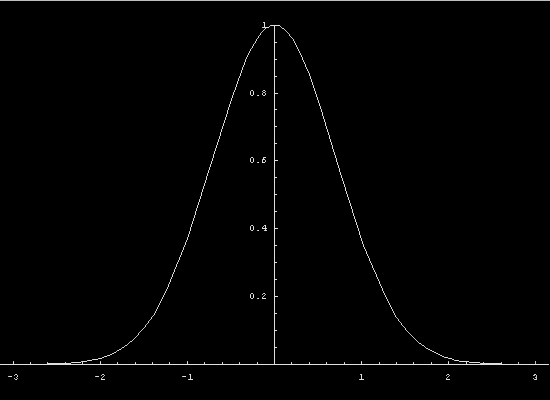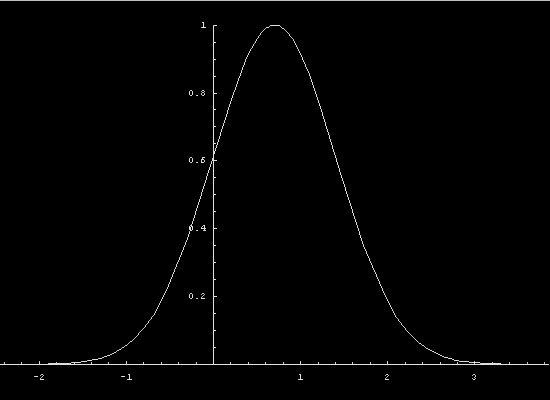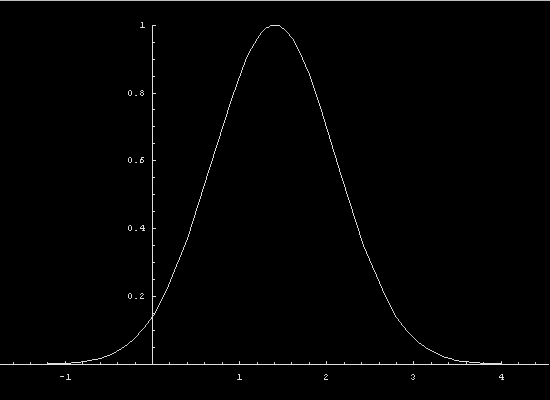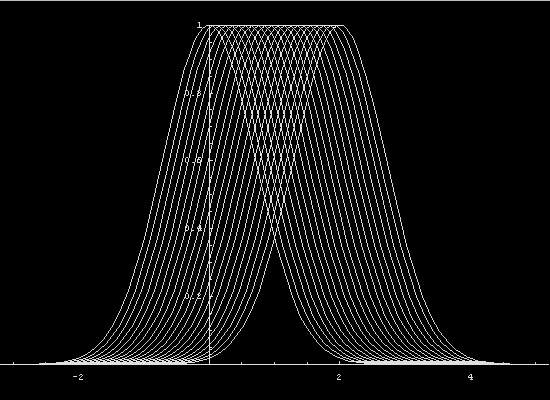
In the nonlinear case, different values of the state variable propagate at different speed and the profile warps. The following movie was created with the help of the mathematica program, shockprofiles.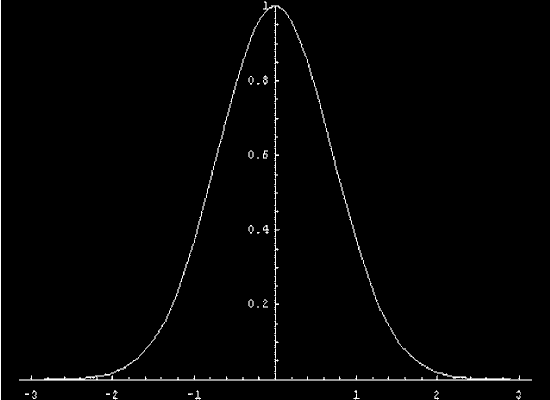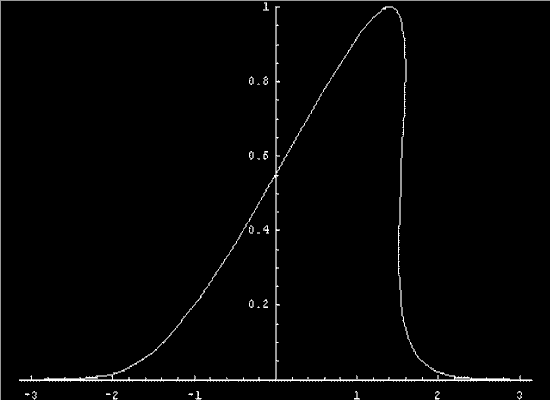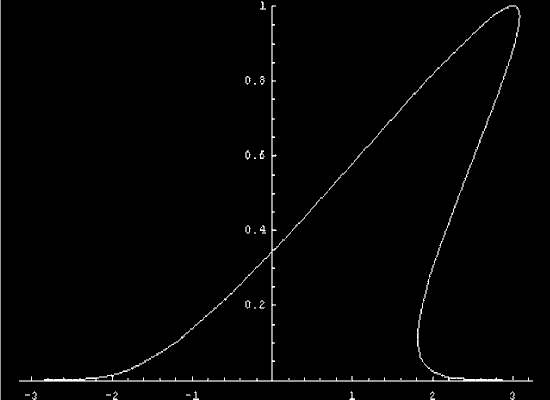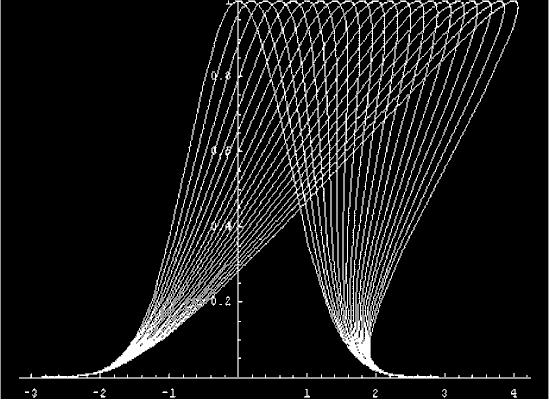

Note that on the phase plane diagrams there exist points where multiple characteristics meet. This does not mean that all characteristics have the same value; it denotes the place where the solution becomes multiple valued. Sometimes a multiple valued solution is desirable. In other cases, multiple states can have no physical interpretation. In these cases, "shockwaves" form. There is a method called the "equal area law" that determines where the discontinuity should be located. See below.