6/21 Week 2: State Space

Weekly meetings were held by Professor Norman in the GANG lab. Each student participating in the REU program was expected to present their work before the group. Our first presentation was made on the second week.

With the shockprofile program and the equal area law, we are able to solve any conservation equation in one variable in one spatial dimension. With multiple state variables, new tools must be developed. We introduce a new diagram, the "state space" diagram. At each point in the phase plane there will be a single value for each state variable. If we take our axes to be the state variables, the set of all states described by our system of differential equations forms a surface.

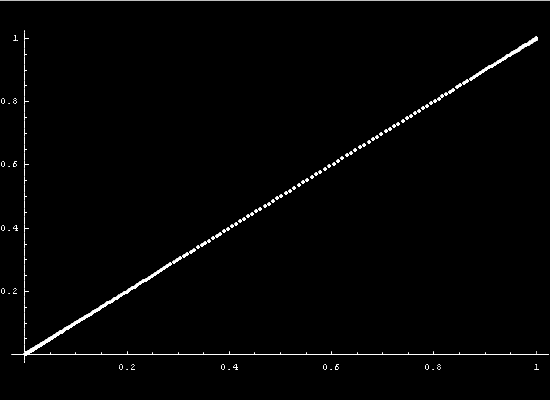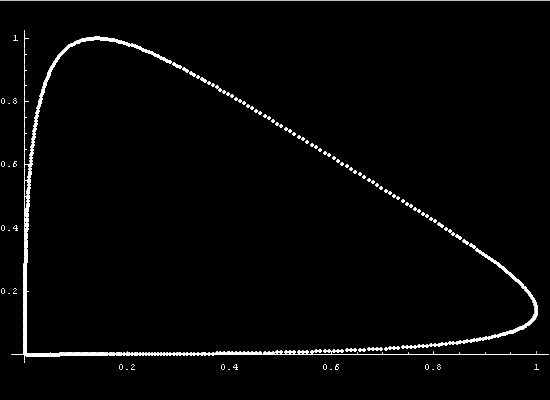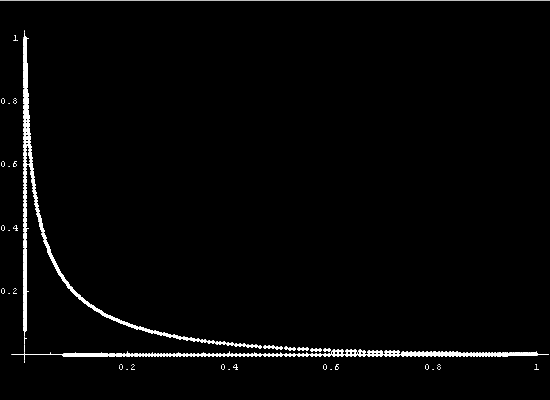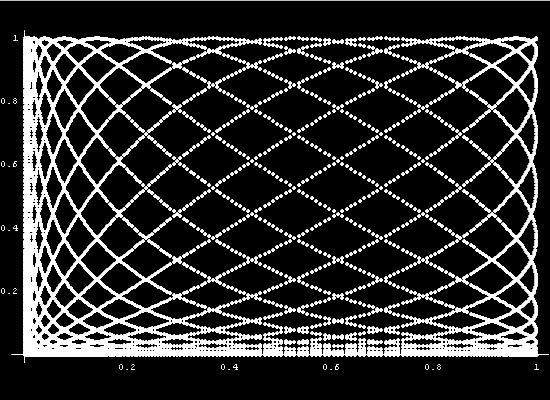
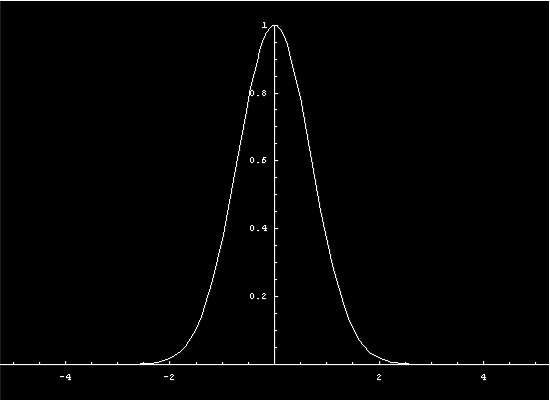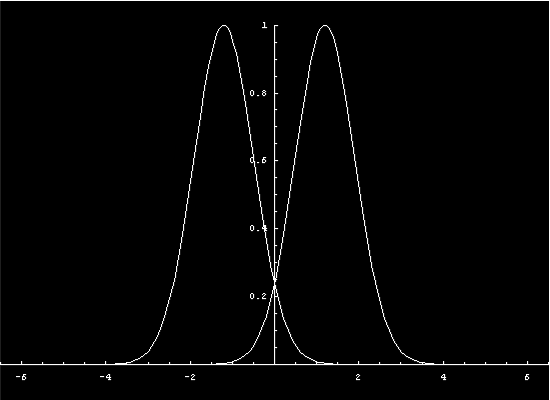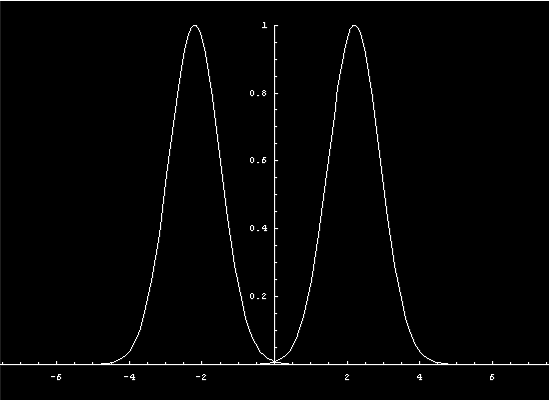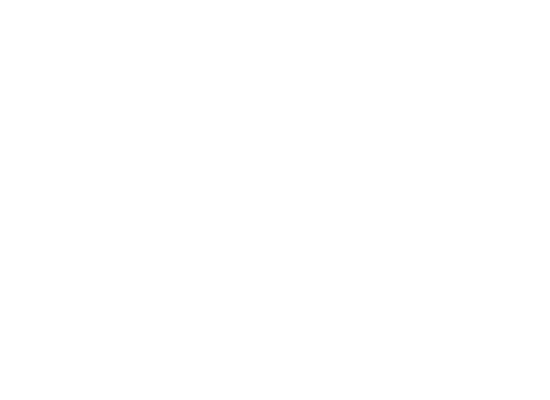
To get a more intuitive feeling for the state space, we wrote a program to model the case of two or three decoupled scalar equations. The curve in state space is a parametric function of x. At each point x the state variables will take on different values. The graphing of those values as a vector function results in the state space diagram. As time passes the system will take on different states.

The two diverging shock profiles were made with the multipleprofiles program.

Given a system of scalar PDEs, one can write the system as a vector conservation law. Using multivariable calculus, one can take the jacobian, or full matrix derivative, of the vector flux function. The derivative of F with respect to the vector U is called the “Flux Matrix.” The eigensystem of this matrix provides important clues as to the behavior of the system.